A spectral-element solver for the incompressible Navier-Stokes equations with thermal coupling
Instructor : Prof. Paul F. Fischer, CS555
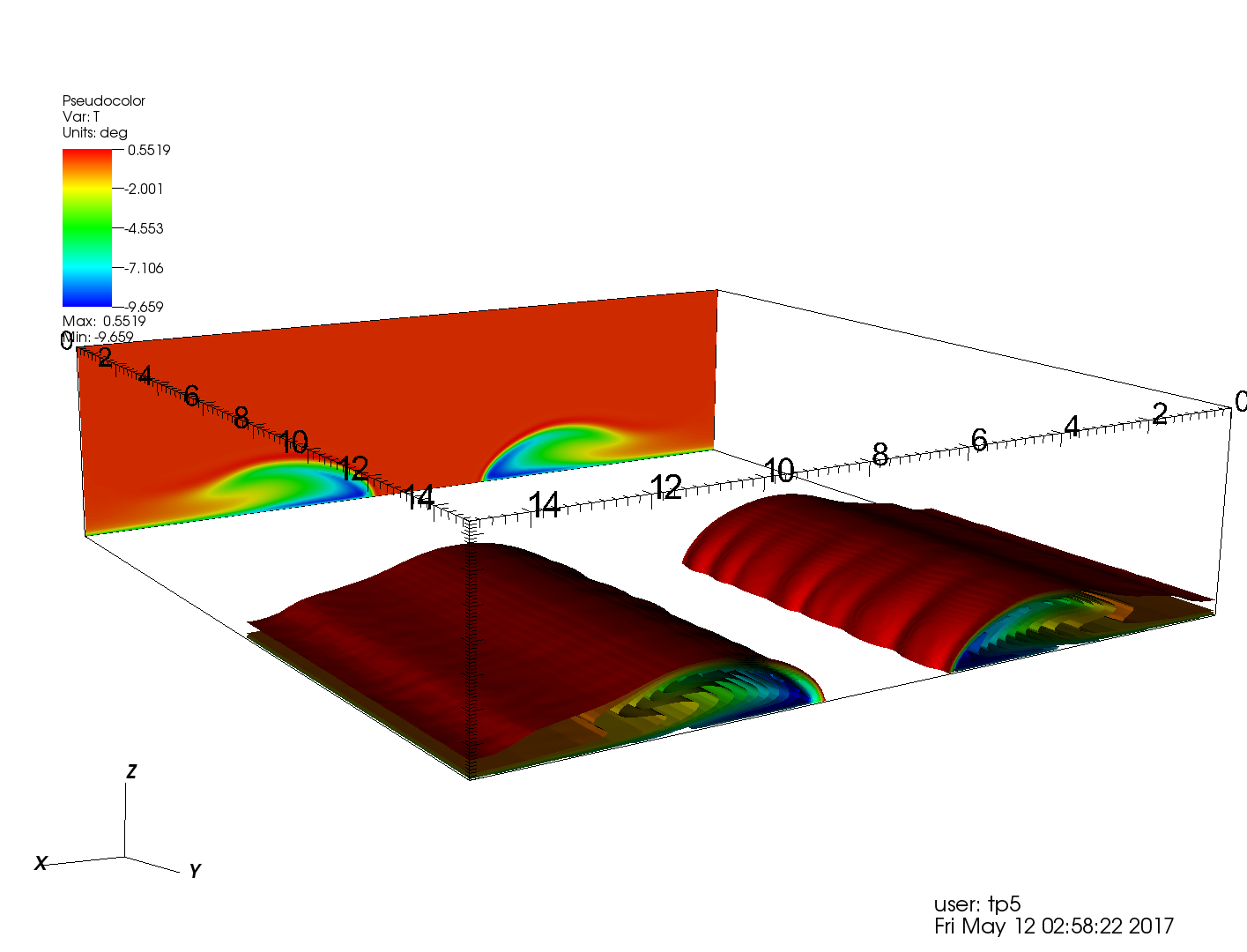
We constructed a (fast!) QN-Q(N-2) spectral element solver for the Navier-Stokes equations and coupled it to the energy equations through the Boussinesq approximation—aiming to predict the critical Rayleigh number for the Rayleigh- Benard convection problem. We presented a poster in the end that briefly describes our solver capabilities—I have attached the same below:
With 50 order polynomials and a single element we could predict the critical Rayleigh number to the first two decimal digits. Here’s an animation of all the fields as they evolve, with periodic boundary conditions on the side walls. You can see the motionless flow tend to the (steady) convective roll solution.

We could also realize a case with the same setup, but with the top wall moving with an unit velocity to the right. In this case we get a mixed Rayleigh-Benard, Kelvin-Helmoltz type instability:

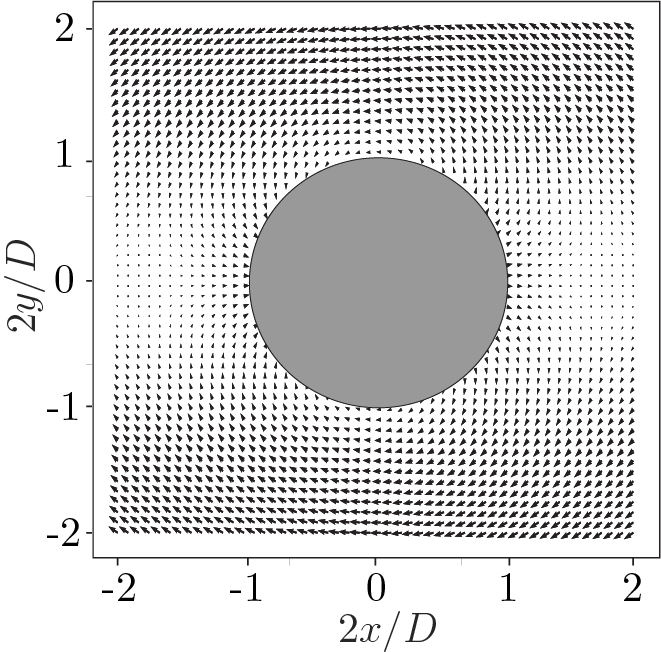
Based on the same infrastructure we also constructed a solver for the Stokes equations (Re tending to zero), but using P2-P1 (Taylor-Hood) finite elements. A picture of the flow due to a cylinder above a moving wall (Wannier flow) is shown below:
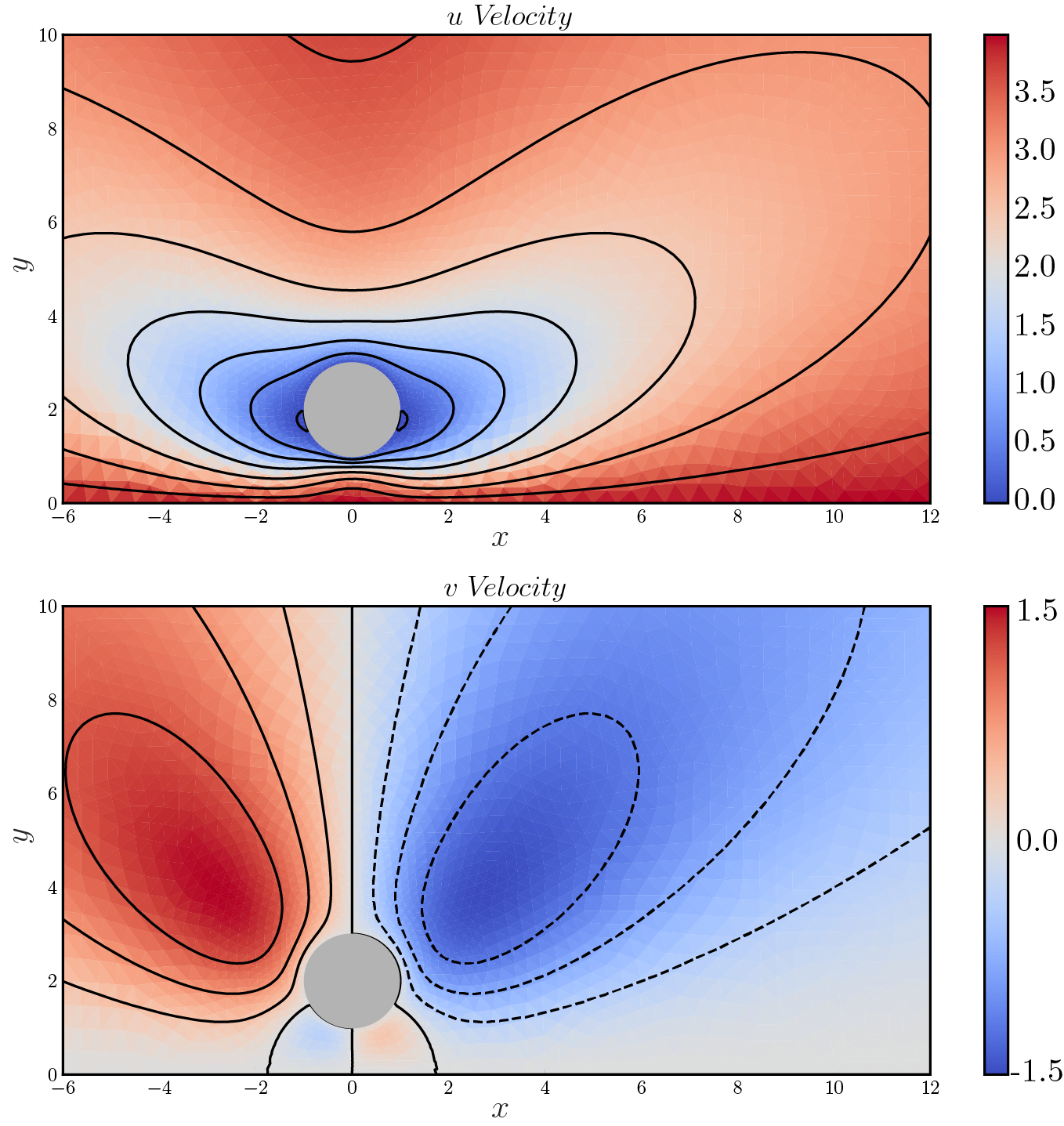
A steady Stokes-PDE solver based on Integral Equation methods
Instructor : Prof. Andreas Klöckner, CS598APK
I learnt to develop a numerical solver for the Stokes flow equations using an integral equation formulation of the PDE, coupled with a subset of ‘fast algorithms’. Robust, fast and accurate numerical solutions for the stokes PDE can be tricky, because it is ‘coupled’ via the incompressibility constraint, which upon discretization leads to ill-conditioned systems (the FEM crowd have developed many ways to overcome this—the most popular of which is using Taylor-Hood elements). Using an integral equation formulation we obtain a ‘double-layer’ representation (for the Neumann problem) for the PDE which leads to a second-kind Fredholm equation. With some algebra, and using Nyström discretization, we get a decoupled matrix-system that can be iteratively solved for. This system has a bounded condition number (independent of the mesh size), is accurate (the errors we commit are related only to finite-representation and quadrature) and extends itself to higher order. Futhermore it requires discretizing only the boundaries (leading to the appropriately named ‘boundary element methods’) and hence very robust. Apart from the savings we get by not generating a volume-mesh in this case, we use a subset of ‘fast algorithms’ that has linear run-time algorithmic complexity! IE methods are hence very capable and useful in any numerical analyst’s toolkit.
A 3-D quasi-compressible Navier-Stokes solver for the simulation of atmospheric phenomena
Instructor : Prof. Brian Jewett, CSE566
I developed a 3-D nonlinear quasi-compressible flow solver using a combination of higher-order finite-difference (FDM) and a piecewise-linear finite-volume method (with Van-Leer reconstruction) for spatial discretization. Temporal discretization was done using explicit and implicit treatment for the slow and fast-scale physics terms via Strang splitting. To improve accuracy, grid staggering was employed. Shared memory parallelism was achieved through OpenMP constructs. An equivalent version for 2-D with Adaptive Mesh Refinement (AMR) capabilities was also implemented.